Matched pair design in statistics involves comparing two related groups. This method controls for variables that may affect the outcome.
Matched pair design, a vital component of experimental research, pairs similar subjects or groups together to minimize variability in the results. Researchers typically use this approach when they want to assess the effects of a specific treatment or intervention by comparing outcomes between the paired groups.
By matching subjects based on key characteristics, this design enhances the accuracy of attributing any observed differences to the factor under investigation rather than to extraneous variables. This statistical method is especially useful in small sample sizes and can be applied across various fields, from medicine to social sciences, providing insightful data for making informed decisions. The precise pairing process and controlled environment this design offers help scientists and researchers isolate the impact of their variables of interest.
Credit: www.simplypsychology.org
Introduction To Matched Pair Design
Delving into the realm of statistics, we often encounter experimental designs that aim to reduce variability and improve the reliability of results. One such approach is the Matched Pair Design. It’s a tactic researchers employ to compare two treatments while minimizing differences between the subjects. Let’s explore this design’s essence and its advantages in research.
Essence Of Matched Pair Design
The core concept of Matched Pair Design lies in its pairing mechanism. By matching subjects based on key characteristics, it ensures that each pair is as similar as possible. This similarity is crucial because it controls confounding variables, focusing solely on the treatment effects. In a Matched Pair Design, one subject from each pair receives one treatment, and the other subject receives another treatment. Researchers often use this design to tease apart the differences that the treatments may elicit.
Advantages In Research Settings
- Improves accuracy: By matching subjects closely, the design reduces the chance of external variables skewing the data.
- Controls variability: It minimizes effects of individual differences that are not related to the treatments being tested.
- Efficient use of data: Matched Pair Design tends to require fewer subjects to achieve statistical significance, making research more time and cost-effective.
- Flexible pairing: Researchers can match subjects on a multitude of characteristics, making it highly adaptable to various studies.
Key Principles Of Matched Pair Design
Understanding the key principles of Matched Pair Design can enhance the accuracy of statistical studies. This design pairs participants closely based on specific criteria. It helps reduce variability and draws clear conclusions on cause-effect relationships. Let’s explore the core principles behind this powerful statistical approach.
Creating Matched Pairs
To ensure credible results, creating matched pairs requires careful attention to detail:
- Identify key characteristics where participants are alike.
- Pair up participants to neutralize confounding variables.
- Use relevant data and metrics to match subjects correctly.
Creating pairs this way leads to more reliable comparisons.
Randomization And Control
Randomization and control play pivotal roles in Matched Pair Design:
| Randomization | Control |
|---|---|
| Assign treatments to pairs randomly. | Manage external factors to maintain consistency. |
| Minimize selection bias. | Ensure the effect is due to the treatment only. |
Together, these principles strengthen the study’s integrity and its findings.
Implementing Matched Pair Design
If you want results you can trust, matched pair design statistics can be a game-changer. This method compares two groups that are alike in many ways. It helps find out if a certain change or treatment causes different results. Now, let’s learn how to put this powerful tool into action.
Selecting Variables For Matching
Choosing the right variables is key to a successful study. Think about the parts of your experiment that could affect the outcome. Here are some steps to select the best variables for matching:
- Identify core characteristics: Look for traits that could sway your findings, like age or gender.
- Analyze past data: Previous studies can show which variables matter most.
- Consider the treatment: Make sure variables match the treatment’s effects.
Pairing Techniques
Once you’ve selected your variables, the next step is pairing. Use these techniques to make pairs that are as close as a twin set:
- Random Pairing: This draws pairs randomly, aiming for a balanced mix.
- Exact Matching: Here, pairs are identical twins in the variables you chose.
- Rank Order: Sort participants, then pair top with top, bottom with bottom.
This table shows the methods side by side:
| Technique | Advantages | Best Used When |
|---|---|---|
| Random Pairing | Simple, fair approach | Large sample sizes |
| Exact Matching | Highly accurate matches | Key variables well-defined |
| Rank Order | Balance without exact matches | Variables have a natural order |
To make sure your matched pair design shines, always review your variables and pairing techniques. Get them right, and you’re on track for trustworthy, valuable results.
Credit: nap.nationalacademies.org
Analyzing Data From Matched Pair Experiments
Matched pair experiments shine in statistical analysis. They allow researchers to compare two sets of data that are linked. But once the experiment ends, the real work begins—analyzing the data. This piece delves into the intricate process of peeling back the layers of matched pair data.
Statistical Tests For Matched Pairs
Choosing the right statistical test is key. It ensures the data speaks the truth. Here are some tests often used:
- t-test for dependent samples: Checks if mean differences are statistically significant.
- Wilcoxon signed-rank test: Non-parametric alternative to the t-test.
- Sign test: Simpler non-parametric test based on direction of change between pairs.
To run a test, you’ll need:
- Data normality check: Ensures data fits the chosen test.
- Paired observations: Confirms data is properly matched.
- Significance level set: Defines the threshold for determining results.
Once these steps are completed, apply the test to interpret your findings.
Interpreting Results
Interpreting results unlocks the experiment’s value. Keep an eye out for these pointers:
| Statistical Term | What It Tells You |
|---|---|
| p-value | Shows if your results are by chance. |
| Confidence Interval | Gives a range in which the true difference likely falls. |
| Effect Size | Indicates how big the difference is. |
Look for a p-value less than 0.05. This often means your findings are strong. A wide confidence interval suggests more data may be needed. A large effect size speaks to the difference’s importance.
Understanding these elements leads to credible conclusions from your matched pair experiment.
Case Studies
Matched pair design statistics offer a unique lens through which researchers can observe the effectiveness of interventions. This design reduces variability and increases the statistical power of the study. By looking at specific case studies, we can explore how this design enhances the reliability of results in various fields.
Matched Pair Design In Clinical Trials
Case studies in clinical trials show how matched pair design elevates research quality. Doctors use it to compare treatments. Patients with similar attributes like age and health status create pairs. One gets the new treatment. The other gets the standard or a placebo. This direct comparison often reveals which treatment works best.
- Better control for variables: Age, gender, and health level in pairs are similar.
- Clearer outcomes: Reduces outside influence on results.
- Increased reliability: Offers robust evidence for new treatments.
Innovative Applications In Social Sciences
Social scientists also leverage matched pair design. They study behaviors and attitudes. Participants with like characteristics form pairs. Researchers observe how different social factors affect them. This method isolates the factor’s effect and minimizes biases.
- Detailed insights: Delivers deeper understanding of social dynamics.
- Reduces bias: Matching on key attributes controls for confounding variables.
- Broader application: Adapts to various social science fields.
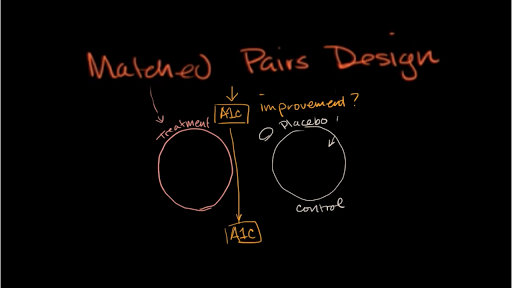
Credit: www.khanacademy.org
Challenges And Considerations
Using Matched Pair Design in statistics is smart. But it has its own set of puzzles to solve. What are these puzzles? Let’s dive in.
Limitations Of Matched Pair Design
Even the best tools have limits. Matched Pair Design is no different.
- Perfect matches are rare. Finding two things that are the same in every way is tough.
- Dropouts can skew results. If subjects leave, it messes up our matching.
- Not for large groups. When we have lots of subjects, this design gets hard.
This design shines in control, but these limitations need careful thought.
Ensuring Validity And Reliability
Validity and reliability are like the North Star in studies; they guide us to truth.
- Keep it tight. Stick to your plan to stop bias.
- Check your pairs. Make sure they really match up.
- Repeat the test. The same results over and again mean it’s reliable.
By focusing on these steps, we steer towards meaningful outcomes.
Frequently Asked Questions For Matched Pair Design Statistics
What Is An Example Of A Matched Pair In Statistics?
A matched pair in statistics occurs when researchers pair subjects based on similar characteristics before applying different treatments. For example, identical twins receiving different diets to study the effects on weight loss.
What Is The Statistical Advantage Of Using A Matched Pairs Design?
A matched pairs design boosts statistical power by reducing variability, ensuring that comparisons between conditions are more precise and require fewer subjects.
What Is A Matched Pair In Ap Stats?
A matched pair in AP Statistics refers to two related observations, often the same subject before and after a treatment, used for comparison in paired samples or experiments.
What Are The Strengths Of Matched Pairs Design?
Matched pairs design increases result accuracy by pairing similar subjects, reducing variability. It enables controlling for participant-specific variables, enhancing statistical power. This method minimizes the impact of confounding variables, leading to stronger, more reliable conclusions.
Conclusion
Understanding matched pair design statistics is crucial for precise data analysis. By recognizing the value of pairing subjects, researchers can significantly reduce variability. This method enhances the accuracy of statistical results, leading to more trustworthy conclusions. Embrace this approach to strengthen your research endeavors and glean meaningful insights from your data sets.
